Forum
Login
Register

Welcome to our Support Center
UpdatedAugust 28, 2025

ScatterND

Description

ScatterND takes three inputsΒ dataΒ tensor of rank r >= 1,Β indicesΒ tensor of rank q >= 1, andΒ updatesΒ tensor of rank q + r – indices.shape[-1] – 1. The output of the operation is produced by creating a copy of the inputΒ data, and then updating its value to values specified byΒ updatesΒ at specific index positions specified byΒ indices. Its output shape is the same as the shape ofΒ data.

 

 

indicesΒ is an integer tensor. Let k denote indices.shape[-1], the last dimension in the shape ofΒ indices.Β indicesΒ is treated as a (q-1)-dimensional tensor of k-tuples, where each k-tuple is a partial-index intoΒ data. Hence, k can be a value at most the rank ofΒ data. When k equals rank(data), each update entry specifies an update to a single element of the tensor. When k is less than rank(data) each update entry specifies an update to a slice of the tensor. Index values are allowed to be negative, as per the usual convention for counting backwards from the end, but are expected in the valid range.

updatesΒ is treated as a (q-1)-dimensional tensor of replacement-slice-values. Thus, the first (q-1) dimensions of updates.shape must match the first (q-1) dimensions of indices.shape. The remaining dimensions ofΒ updatesΒ correspond to the dimensions of the replacement-slice-values. Each replacement-slice-value is a (r-k) dimensional tensor, corresponding to the trailing (r-k) dimensions ofΒ data. Thus, the shape ofΒ updatesΒ must equal indices.shape[0:q-1] ++ data.shape[k:r-1], where ++ denotes the concatenation of shapes.

TheΒ outputΒ is calculated via the following equation:

output = np.copy(data)
update_indices = indices.shape[:-1]
for idx in np.ndindex(update_indices):
    output[indices[idx]] = updates[idx]

The order of iteration in the above loop is not specified. In particular, indices should not have duplicate entries: that is, if idx1 != idx2, then indices[idx1] != indices[idx2]. This ensures that the output value does not depend on the iteration order.

reductionΒ allows specification of an optional reduction operation, which is applied to all values inΒ updatesΒ tensor intoΒ outputΒ at the specifiedΒ indices. In cases whereΒ reductionΒ is set to β€œnone”, indices should not have duplicate entries: that is, if idx1 != idx2, then indices[idx1] != indices[idx2]. This ensures that the output value does not depend on the iteration order. WhenΒ reductionΒ is set to some reduction functionΒ f,Β outputΒ is calculated as follows:

output = np.copy(data)
update_indices = indices.shape[:-1]
for idx in np.ndindex(update_indices):
    output[indices[idx]] = f(output[indices[idx]], updates[idx])

where theΒ fΒ isΒ +,Β *,Β maxΒ orΒ minΒ as specified.

This operator is the inverse of GatherND.

 

 

Input parameters

 

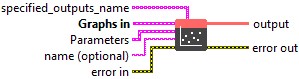
specified_outputs_name :Β array, this parameter lets you manually assign custom names to the output tensors of a node.

Β Graphs in :Β cluster, ONNX model architecture.

data (heterogeneous) – T : object, tensor of rank r >= 1.
indices (heterogeneous) – tensor(int64) : object, tensor of rank q >= 1.
updates (heterogeneous) – T : object, tensor of rank q + r – indices_shape[-1] – 1.

Β Parameters :Β cluster,

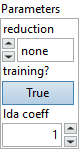
reduction : enum, type of reduction to apply: none (default), add, mul, max, min. β€˜none’: no reduction applied. β€˜add’: reduction using the addition operation. β€˜mul’: reduction using the addition operation. β€˜max’: reduction using the maximum operation.β€˜min’: reduction using the minimum operation.
Default value β€œnone”.
Β training?Β :Β boolean, whether the layer is in training mode (can store data for backward).
Default value β€œTrue”.
Β lda coeff :Β float, defines the coefficient by which the loss derivative will be multiplied before being sent to the previous layer (since during the backward run we go backwards).
Default value β€œ1”.

Β name (optional) :Β string,Β name of the node.

Output parameters

output (heterogeneous) – T : object, tensor of rank r >= 1.

Type Constraints

T in (tensor(bfloat16),Β tensor(bool),Β tensor(complex128),Β tensor(complex64),Β tensor(double),Β tensor(float),Β tensor(float16),Β 
tensor(int16),Β tensor(int32),Β tensor(int64),Β tensor(int8),Β tensor(string),Β tensor(uint16),Β tensor(uint32),Β tensor(uint64),Β tensor(uint8)) : Constrain input and output types to any tensor type.

Example

All these exemples are snippets PNG, you can drop these Snippet onto the block diagram and get the depicted code added to your VI (Do not forget to install Deep Learning library to run it).
Table of Contents