-
SOTA
-
Accelerator Toolkit
-
Deep Learning Toolkit
-
-
- Resume
- Add
- AlphaDropout
- AdditiveAttention
- Attention
- Average
- AvgPool1D
- AvgPool2D
- AvgPool3D
- BatchNormalization
- Bidirectional
- Concatenate
- Conv1D
- Conv1DTranspose
- Conv2D
- Conv2DTranspose
- Conv3D
- Conv3DTranspose
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Dense
- Cropping1D
- Cropping2D
- Cropping3D
- DepthwiseConv2D
- Dropout
- Embedding
- Flatten
- ELU
- Exponential
- GaussianDropout
- GaussianNoise
- GlobalAvgPool1D
- GlobalAvgPool2D
- GlobalAvgPool3D
- GlobalMaxPool1D
- GlobalMaxPool2D
- GlobalMaxPool3D
- GRU
- GELU
- Input
- LayerNormalization
- LSTM
- MaxPool1D
- MaxPool2D
- MaxPool3D
- MultiHeadAttention
- HardSigmoid
- LeakyReLU
- Linear
- Multiply
- Permute3D
- Reshape
- RNN
- PReLU
- ReLU
- SELU
- Output Predict
- Output Train
- SeparableConv1D
- SeparableConv2D
- SimpleRNN
- SpatialDropout
- Sigmoid
- SoftMax
- SoftPlus
- SoftSign
- Split
- UpSampling1D
- UpSampling2D
- UpSampling3D
- ZeroPadding1D
- ZeroPadding2D
- ZeroPadding3D
- Swish
- TanH
- ThresholdedReLU
- Substract
- Show All Articles (63) Collapse Articles
-
-
-
-
- Exp
- Identity
- Abs
- Acos
- Acosh
- ArgMax
- ArgMin
- Asin
- Asinh
- Atan
- Atanh
- AveragePool
- Bernouilli
- BitwiseNot
- BlackmanWindow
- Cast
- Ceil
- Celu
- ConcatFromSequence
- Cos
- Cosh
- DepthToSpace
- Det
- DynamicTimeWarping
- Erf
- EyeLike
- Flatten
- Floor
- GlobalAveragePool
- GlobalLpPool
- GlobalMaxPool
- HammingWindow
- HannWindow
- HardSwish
- HardMax
- lrfft
- lsNaN
- Log
- LogSoftmax
- LpNormalization
- LpPool
- LRN
- MeanVarianceNormalization
- MicrosoftGelu
- Mish
- Multinomial
- MurmurHash3
- Neg
- NhwcMaxPool
- NonZero
- Not
- OptionalGetElement
- OptionalHasElement
- QuickGelu
- RandomNormalLike
- RandomUniformLike
- RawConstantOfShape
- Reciprocal
- ReduceSumInteger
- RegexFullMatch
- Rfft
- Round
- SampleOp
- Shape
- SequenceLength
- Shrink
- Sin
- Sign
- Sinh
- Size
- SpaceToDepth
- Sqrt
- StringNormalizer
- Tan
- TfldfVectorizer
- Tokenizer
- Transpose
- UnfoldTensor
- lslnf
- ImageDecoder
- Inverse
- Show All Articles (65) Collapse Articles
-
-
-
- Add
- AffineGrid
- And
- BiasAdd
- BiasGelu
- BiasSoftmax
- BiasSplitGelu
- BitShift
- BitwiseAnd
- BitwiseOr
- BitwiseXor
- CastLike
- CDist
- CenterCropPad
- Clip
- Col2lm
- ComplexMul
- ComplexMulConj
- Compress
- ConvInteger
- Conv
- ConvTranspose
- ConvTransposeWithDynamicPads
- CropAndResize
- CumSum
- DeformConv
- DequantizeBFP
- DequantizeLinear
- DequantizeWithOrder
- DFT
- Div
- DynamicQuantizeMatMul
- Equal
- Expand
- ExpandDims
- FastGelu
- FusedConv
- FusedGemm
- FusedMatMul
- FusedMatMulActivation
- GatedRelativePositionBias
- Gather
- GatherElements
- GatherND
- Gemm
- GemmFastGelu
- GemmFloat8
- Greater
- GreaterOrEqual
- GreedySearch
- GridSample
- GroupNorm
- InstanceNormalization
- Less
- LessOrEqual
- LongformerAttention
- MatMul
- MatMulBnb4
- MatMulFpQ4
- MatMulInteger
- MatMulInteger16
- MatMulIntergerToFloat
- MatMulNBits
- MaxPoolWithMask
- MaxRoiPool
- MaxUnPool
- MelWeightMatrix
- MicrosoftDequantizeLinear
- MicrosoftGatherND
- MicrosoftGridSample
- MicrosoftPad
- MicrosoftQLinearConv
- MicrosoftQuantizeLinear
- MicrosoftRange
- MicrosoftTrilu
- Mod
- MoE
- Mul
- MulInteger
- NegativeLogLikelihoodLoss
- NGramRepeatBlock
- NhwcConv
- NhwcFusedConv
- NonMaxSuppression
- OneHot
- Or
- PackedAttention
- PackedMultiHeadAttention
- Pad
- Pow
- QGemm
- QLinearAdd
- QLinearAveragePool
- QLinearConcat
- QLinearConv
- QLinearGlobalAveragePool
- QLinearLeakyRelu
- QLinearMatMul
- QLinearMul
- QLinearReduceMean
- QLinearSigmoid
- QLinearSoftmax
- QLinearWhere
- QMoE
- QOrderedAttention
- QOrderedGelu
- QOrderedLayerNormalization
- QOrderedLongformerAttention
- QOrderedMatMul
- QuantizeLinear
- QuantizeWithOrder
- Range
- ReduceL1
- ReduceL2
- ReduceLogSum
- ReduceLogSumExp
- ReduceMax
- ReduceMean
- ReduceMin
- ReduceProd
- ReduceSum
- ReduceSumSquare
- RelativePositionBias
- Reshape
- Resize
- RestorePadding
- ReverseSequence
- RoiAlign
- RotaryEmbedding
- ScatterElements
- ScatterND
- SequenceAt
- SequenceErase
- SequenceInsert
- Sinh
- Slice
- SparseToDenseMatMul
- SplitToSequence
- Squeeze
- STFT
- StringConcat
- Sub
- Tile
- TorchEmbedding
- TransposeMatMul
- Trilu
- Unsqueeze
- Where
- WordConvEmbedding
- Xor
- Show All Articles (134) Collapse Articles
-
- Attention
- AttnLSTM
- BatchNormalization
- BiasDropout
- BifurcationDetector
- BitmaskBiasDropout
- BitmaskDropout
- DecoderAttention
- DecoderMaskedMultiHeadAttention
- DecoderMaskedSelfAttention
- Dropout
- DynamicQuantizeLinear
- DynamicQuantizeLSTM
- EmbedLayerNormalization
- GemmaRotaryEmbedding
- GroupQueryAttention
- GRU
- LayerNormalization
- LSTM
- MicrosoftMultiHeadAttention
- QAttention
- RemovePadding
- RNN
- Sampling
- SkipGroupNorm
- SkipLayerNormalization
- SkipSimplifiedLayerNormalization
- SoftmaxCrossEntropyLoss
- SparseAttention
- TopK
- WhisperBeamSearch
- Show All Articles (15) Collapse Articles
-
-
-
-
-
-
-
-
-
-
- AdditiveAttention
- Attention
- BatchNormalization
- Bidirectional
- Conv1D
- Conv2D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Dense
- DepthwiseConv2D
- Embedding
- LayerNormalization
- GRU
- LSTM
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- MutiHeadAttention
- SeparableConv1D
- SeparableConv2D
- MultiHeadAttention
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- 1D
- 2D
- 3D
- 4D
- 5D
- 6D
- Scalar
- Show All Articles (22) Collapse Articles
-
- AdditiveAttention
- Attention
- BatchNormalization
- Conv1D
- Conv2D
- Conv1DTranspose
- Conv2DTranspose
- Bidirectional
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv3DTranspose
- DepthwiseConv2D
- Dense
- Embedding
- LayerNormalization
- GRU
- PReLU 2D
- PReLU 3D
- PReLU 4D
- MultiHeadAttention
- LSTM
- PReLU 5D
- SeparableConv1D
- SeparableConv2D
- SimpleRNN
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- 1D
- 2D
- 3D
- 4D
- 5D
- 6D
- Scalar
- Show All Articles (21) Collapse Articles
-
-
- AdditiveAttention
- Attention
- BatchNormalization
- Bidirectional
- Conv1D
- Conv2D
- Conv3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Dense
- DepthwiseConv2D
- Embedding
- GRU
- LayerNormalization
- LSTM
- MultiHeadAttention
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Resume
- SeparableConv1D
- SeparableConv2D
- SimpleRNN
- Show All Articles (12) Collapse Articles
-
-
- Dense
- Embedding
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- BatchNormalization
- LayerNormalization
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Bidirectional
- GRU
- LSTM
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- PReLU 4D
- Show All Articles (15) Collapse Articles
-
- Dense
- Embedding
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- BatchNormalization
- LayerNormalization
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Bidirectional
- GRU
- LSTM
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- Show All Articles (14) Collapse Articles
-
-
- Accuracy
- BinaryAccuracy
- BinaryCrossentropy
- BinaryIoU
- CategoricalAccuracy
- CategoricalCrossentropy
- CategoricalHinge
- CosineSimilarity
- FalseNegatives
- FalsePositives
- Hinge
- Huber
- IoU
- KLDivergence
- LogCoshError
- Mean
- MeanAbsoluteError
- MeanAbsolutePercentageError
- MeanIoU
- MeanRelativeError
- MeanSquaredError
- MeanSquaredLogarithmicError
- MeanTensor
- OneHotIoU
- OneHotMeanIoU
- Poisson
- Precision
- PrecisionAtRecall
- Recall
- RecallAtPrecision
- RootMeanSquaredError
- SensitivityAtSpecificity
- SparseCategoricalAccuracy
- SparseCategoricalCrossentropy
- SparseTopKCategoricalAccuracy
- Specificity
- SpecificityAtSensitivity
- SquaredHinge
- Sum
- TopKCategoricalAccuracy
- TrueNegatives
- TruePositives
- Resume
- Show All Articles (27) Collapse Articles
-
-
- Dense
- Embedding
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- BatchNormalization
- LayerNormalization
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Bidirectional
- GRU
- LSTM
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- Show All Articles (14) Collapse Articles
-
- Dense
- Embedding
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- LayerNormalization
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Bidirectional
- GRU
- LSTM
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- BatchNormalization
- Show All Articles (14) Collapse Articles
-
-
-
Computer Vision Toolkit
-
CUDA Toolkit
-
- Resume
- Array size
- Index Array
- Replace Subset
- Insert Into Array
- Delete From Array
- Initialize Array
- Build Array
- Concatenate Array
- Array Subset
- Min & Max
- Reshape Array
- Short Array
- Reverse 1D array
- Shuffle array
- Search In Array
- Split 1D Array
- Split 2D Array
- Rotate 1D Array
- Increment Array Element
- Decrement Array Element
- Interpolate 1D Array
- Threshold 1D Array
- Interleave 1D Array
- Decimate 1D Array
- Transpose Array
- Remove Duplicate From 1D Array
- Show All Articles (11) Collapse Articles
-
-
- Resume
- Add
- Substract
- Multiply
- Divide
- Quotient & Remainder
- Increment
- Decrement
- Add Array Element
- Multiply Array Element
- Absolute
- Round To Nearest
- Round Toward -Infinity
- Round Toward +Infinity
- Scale By Power Of Two
- Square Root
- Square
- Negate
- Reciprocal
- Sign
- Show All Articles (4) Collapse Articles
GridSample
Description
Given an input X and a flow-field grid, computes the output Y using X values and pixel locations from the grid.
For spatial input X with shape (N, C, H, W), the grid will have shape (N, H_out, W_out, 2), the output Y will have shape (N, C, H_out, W_out). For volumetric input X with shape (N, C, D, H, W), the grid will have shape (N, D_out, H_out, W_out, 3), the output Y will have shape (N, C, D_out, H_out, W_out). More generally, for an input X of rank r+2 with shape (N, C, d1, d2, …, dr), the grid will have shape (N, D1_out, D2_out, …, Dr_out, r), the output Y will have shape (N, C, D1_out, D2_out, …, Dr_out).
The tensor X contains values at centers of square pixels (voxels, etc) locations such as (n, c, d1_in, d2_in, …, dr_in). The (n, d1_out, d2_out, …, dr_out, values from the tensor grid are the normalized positions for interpolating the values at the (n, c, d1_out, d2_out, …, dr_out) locations from the output tensor Y using a specified interpolation method (the mode) and a padding mode (for grid positions falling outside the 2-dimensional image).
For example, the values in grid[n, h_out, w_out, :] are size-2 vectors specifying normalized positions in the 2-dimensional space of X. They are used to interpolate output values of Y[n, c, h_out, w_out].
The GridSample operator is often used in doing grid generator and sampler in the Spatial Transformer Networks. See also in torch.nn.functional.grid_sample.
Input parameters
![]() specified_outputs_name : array, this parameter lets you manually assign custom names to the output tensors of a node.
specified_outputs_name : array, this parameter lets you manually assign custom names to the output tensors of a node.
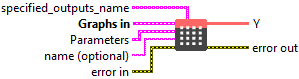
![]() Graphs in : cluster, ONNX model architecture.
Graphs in : cluster, ONNX model architecture.
![]() X (heterogeneous) – T1 : object, input tensor of rank r+2 that has shape (N, C, D1, D2, …, Dr), where N is the batch size, C is the number of channels, D1, D2, …, Dr are the spatial dimensions.
X (heterogeneous) – T1 : object, input tensor of rank r+2 that has shape (N, C, D1, D2, …, Dr), where N is the batch size, C is the number of channels, D1, D2, …, Dr are the spatial dimensions.![]() grid (heterogeneous) – T2 : object, input offset of shape (N, D1_out, D2_out, …, Dr_out, r), where D1_out, D2_out, …, Dr_out are the spatial dimensions of the grid and output, and r is the number of spatial dimensions. Grid specifies the sampling locations normalized by the input spatial dimensions. Therefore, it should have most values in the range of [-1, 1]. If the grid has values outside the range of [-1, 1], the corresponding outputs will be handled as defined by padding_mode. Following computer vision convention, the coordinates in the length-r location vector are listed from the innermost tensor dimension to the outermost, the opposite of regular tensor indexing.
grid (heterogeneous) – T2 : object, input offset of shape (N, D1_out, D2_out, …, Dr_out, r), where D1_out, D2_out, …, Dr_out are the spatial dimensions of the grid and output, and r is the number of spatial dimensions. Grid specifies the sampling locations normalized by the input spatial dimensions. Therefore, it should have most values in the range of [-1, 1]. If the grid has values outside the range of [-1, 1], the corresponding outputs will be handled as defined by padding_mode. Following computer vision convention, the coordinates in the length-r location vector are listed from the innermost tensor dimension to the outermost, the opposite of regular tensor indexing.

![]() Parameters : cluster,
Parameters : cluster,
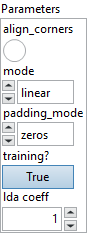
![]() align_corners : boolean, if align_corners=true, the extrema (-1 and 1) are considered as referring to the center points of the input’s corner pixels (voxels, etc.). If align_corners=false, they are instead considered as referring to the corner points of the input’s corner pixels (voxels, etc.), making the sampling more resolution agnostic.
align_corners : boolean, if align_corners=true, the extrema (-1 and 1) are considered as referring to the center points of the input’s corner pixels (voxels, etc.). If align_corners=false, they are instead considered as referring to the corner points of the input’s corner pixels (voxels, etc.), making the sampling more resolution agnostic.
Default value “False”.![]() mode : enum, three interpolation modes: linear (default), nearest and cubic. The “linear” mode includes linear and N-linear interpolation modes depending on the number of spatial dimensions of the input tensor (i.e. linear for 1 spatial dimension, bilinear for 2 spatial dimensions, etc.). The “cubic” mode also includes N-cubic interpolation modes following the same rules. The “nearest” mode rounds to the nearest even index when the sampling point falls halfway between two indices.
mode : enum, three interpolation modes: linear (default), nearest and cubic. The “linear” mode includes linear and N-linear interpolation modes depending on the number of spatial dimensions of the input tensor (i.e. linear for 1 spatial dimension, bilinear for 2 spatial dimensions, etc.). The “cubic” mode also includes N-cubic interpolation modes following the same rules. The “nearest” mode rounds to the nearest even index when the sampling point falls halfway between two indices.
Default value “linear”.![]() padding_mode : enum, support padding modes for outside grid values:
padding_mode : enum, support padding modes for outside grid values: zeros(default), border, reflection. zeros: use 0 for out-of-bound grid locations, border: use border values for out-of-bound grid locations, reflection: use values at locations reflected by the border for out-of-bound grid locations. If index 0 represents the margin pixel, the reflected value at index -1 will be the same as the value at index 1. For location far away from the border, it will keep being reflected until becoming in bound. If pixel location x = -3.5 reflects by border -1 and becomes x’ = 1.5, then reflects by border 1 and becomes x’’ = 0.5.
Default value “zeros”.![]() training? : boolean, whether the layer is in training mode (can store data for backward).
training? : boolean, whether the layer is in training mode (can store data for backward).
Default value “True”.![]() lda coeff : float, defines the coefficient by which the loss derivative will be multiplied before being sent to the previous layer (since during the backward run we go backwards).
lda coeff : float, defines the coefficient by which the loss derivative will be multiplied before being sent to the previous layer (since during the backward run we go backwards).
Default value “1”.
![]() name (optional) : string, name of the node.
name (optional) : string, name of the node.
Output parameters
![]() Y (heterogeneous) – T1 : object, output tensor of rank r+2 that has shape (N, C, D1_out, D2_out, …, Dr_out) of the sampled values. For integer input types, intermediate values are computed as floating point and cast to integer at the end.
Y (heterogeneous) – T1 : object, output tensor of rank r+2 that has shape (N, C, D1_out, D2_out, …, Dr_out) of the sampled values. For integer input types, intermediate values are computed as floating point and cast to integer at the end.
Type Constraints
T1 in (tensor(bool), tensor(complex128), tensor(complex64), tensor(double), tensor(float), tensor(float16), tensor(int16), tensor(int32), tensor(int64), tensor(int8), tensor(string), tensor(uint16), tensor(uint32), tensor(uint64), tensor(uint8)) : Constrain input X and output Y types to all tensor types.
T2 in (tensor(double), tensor(float), tensor(float16)) : Constrain grid types to float tensors.
